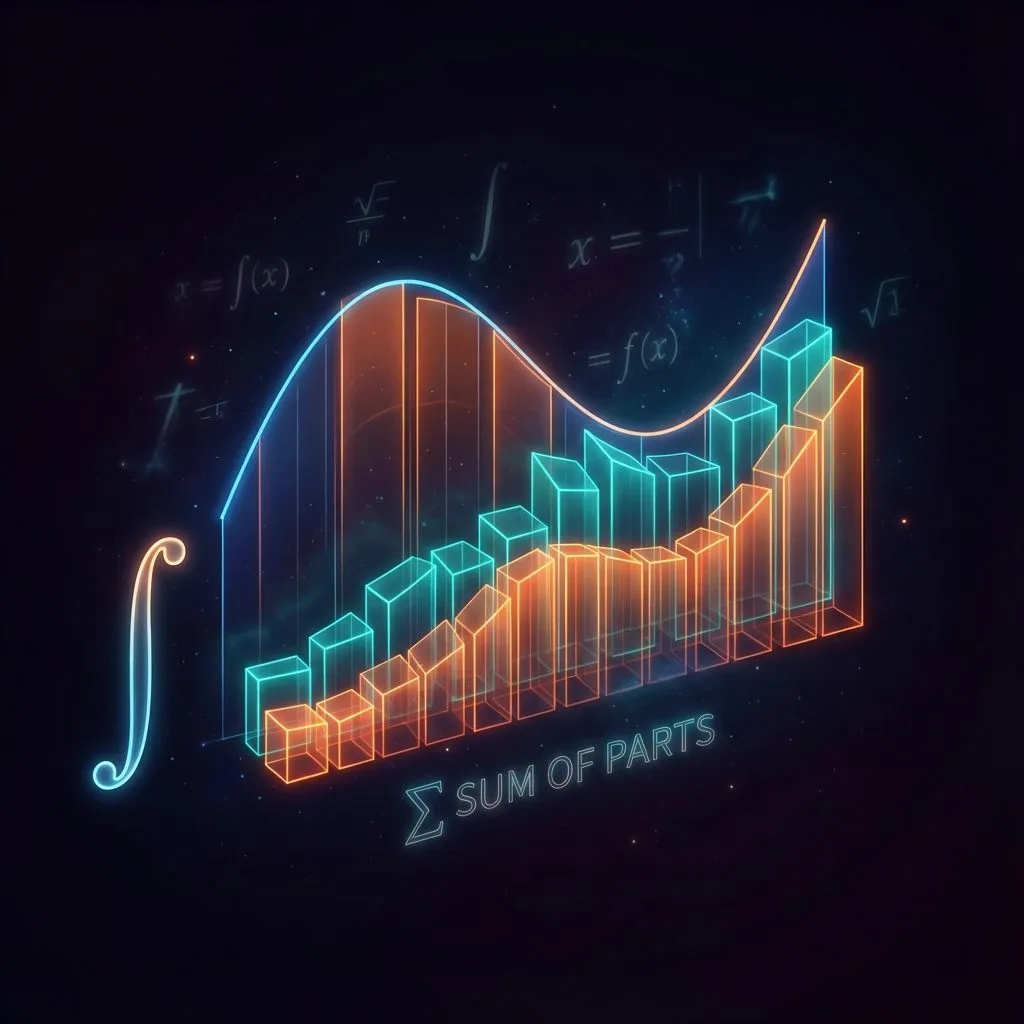
Integration is the superpower of "adding things up". While addition works for finite things (like apples in a basket), Integration works for infinite things (like water flowing into a tank, or distance traveled at varying speeds).

It is the reverse of differentiation. If Differentiation slices a loaf of bread into atoms, Integration glues them back together to recreate the loaf.

1. Riemann Sums (The Rectangle Method)

Before integrals existed, mathematicians used Riemann Sums. Imagine trying to find the area under a curvy hill.

• Step 1: Draw a bunch of rectangles under the curve.
• Step 2: Calculate `Height * Width` for each.
• Step 3: Add them up.

If you use 5 big rectangles, your answer is "blocky" and wrong. If you use 1,000,000 tiny rectangles, your answer is nearly perfect.
The Integral ∫ is simply the sum of infinite, infinitely thin rectangles.

2. The Fundamental Theorem of Calculus

This theorem changed human history. Isaac Newton and Gottfried Leibniz discovered that Area (Integration) and Slope (Differentiation) are inverses. They undo each other.

This means you don't need to draw rectangles to find the area under x². You just need to find the function that has x² as its derivative (which is x³/3). This trick turns geometry problems into algebra problems.

3. Definite vs. Indefinite Integrals

Students often confuse these two.

• Indefinite Integral (No bounds): The answer is a Function. It represents the general family of anti-derivatives. Always add + C.
• Definite Integral (With bounds a to b): The answer is a Number. It represents the specific area between x=a and x=b.

4. Standard Integration Rules

Memorize these or you will fail the exam.

1. Power Rule (Reverse): Add 1 to exponent, divide by new exponent.
∫ x^n dx = (x^(n+1))/(n+1)

2. Logarithm Rule:
∫ (1/x) dx = ln|x|

3. Exponential Rule:
∫ e^x dx = e^x

5. Methods for Harder Integrals

Sometimes the rules aren't enough.

• U-Substitution: The reverse Chain Rule. You replace a messy chunk of the equation with 'u' to make it simpler.
• Integration by Parts: The reverse Product Rule. Formula: ∫ u dv = uv - ∫ v du.
• Partial Fractions: Breaking a big fraction into smaller, simpler fractions.

6. Real World Applications

Physics (Kinematics):
• Integral of Acceleration = Velocity.
• Integral of Velocity = Position.
If you know how hard a rocket engine pushes (Force -> Acceleration), you can integrate twice to figure out exactly where the rocket will be in 10 minutes.

Economics (Total Cost):
Marginal cost is the cost to produce one more item. If you integrate the Marginal Cost function, you get the Total Cost of production.

7. FAQ

Q: Why do I need the +C?
A: Imagine integrating Velocity to get Position. The integral tells you how far you moved. But it doesn't tell you where you started. The +C is your starting point (Initial Condition).

Q: Can integrals be negative?
A: Yes! Area below the x-axis is considered negative area. If you run forward 10m (positive) and backward 10m (negative), your total displacement (integral) is 0.

Conclusion

Integration is the mathematics of accumulation. It allows us to tally up continuous changes over time to find totals—total distance, total volume, total energy. It is the heavy lifter of engineering.