Trigonometry is often viewed as the scary part of high school math. It involves strange words like SOH CAH TOA, Greek letters like Theta (θ), and circles that somehow relate to triangles. But at its core, trigonometry is simply the science of patterns.

It is the mathematics of how things oscillate, vibrate, and rotate. Without trigonometry, we wouldn't have music files (MP3s), GPS navigation, flight simulators, or even the JPEG images you see on this website. In this comprehensive guide, we'll strip away the confusion and look at the engine that powers modern geometry.

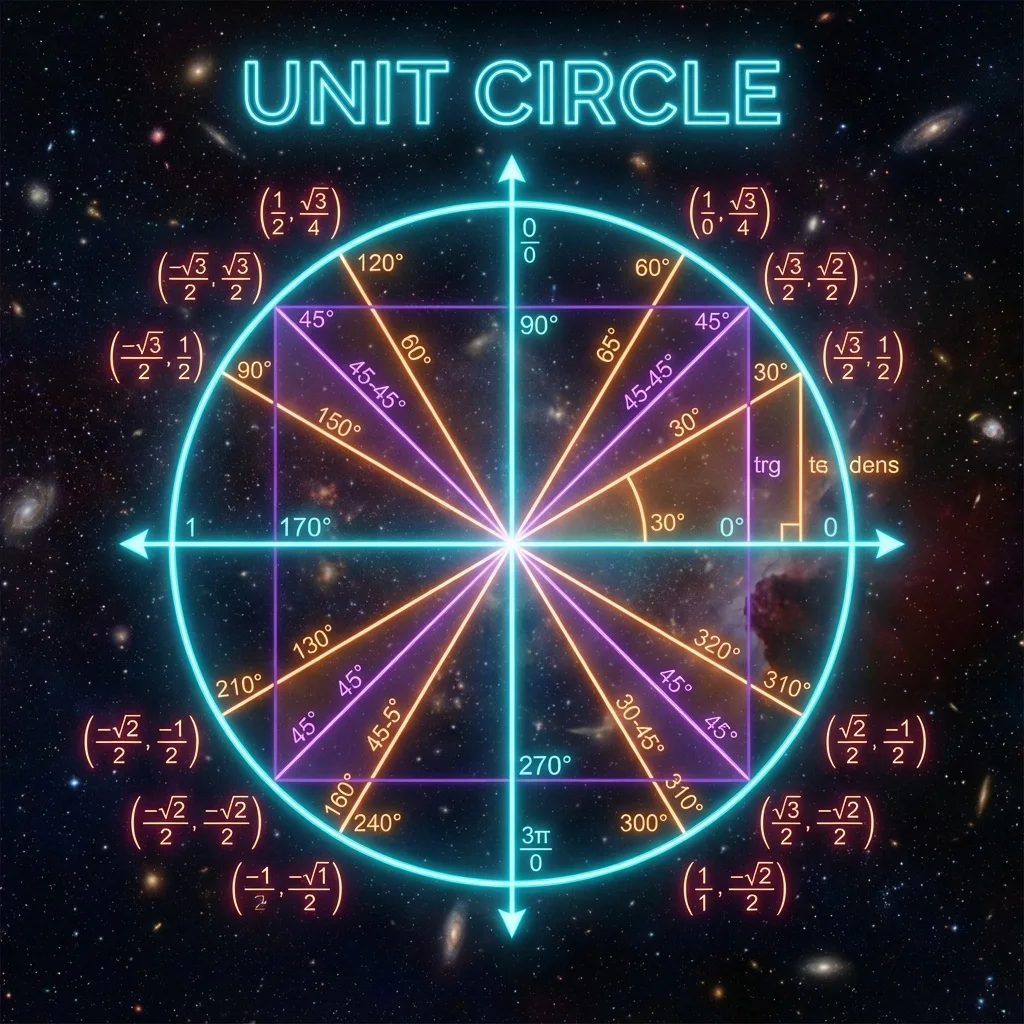
1. The Unit Circle: The "Rosetta Stone"

Most students are introduced to sine and cosine via right-angled triangles. This is great for building bridges, but it limits your understanding to angles less than 90 degrees. How can you have the cosine of 120 degrees? A triangle can't have an angle that big!

Enter the Unit Circle. Imagine a circle with a radius of exactly 1 centered at (0,0) on a graph. If you draw a line from the center to any point on the edge:

• The X-coordinate is the Cosine.
• The Y-coordinate is the Sine.
• The Slope of the line is the Tangent.

This definition works for ANY angle, even negatives or angles bigger than 360/720. This is why sine and cosine look like waves when you graph them—they are just tracking the up-and-down height of a point spinning around a circle.

2. The Big Three: SOH CAH TOA

For practical engineering, the right-triangle definition is king. Whether you are cutting wood for a roof truss or calculating the height of a tree without climbing it, you need these three ratios:

Memory Tip: Imagine an old Native American chief named 'SohCahToa'. Say it out loud. It sticks. Or use a mnemonic: "Some Old Hippie, Caught Another Hippie, Tripping On Acid."

3. The Hidden World of Sound (Waves)

Did you know your noise-canceling headphones use trigonometry? Sound is a pressure wave. It looks exactly like a Sine graph.

Phase Cancellation:
To cancel out noise, the headphones listen to the incoming sound wave (Sine A) and instantly generate an inverse wave (Sine -A). When you add them together (Sine A + Sine -A), you get zero. Silence.

Music producers use this constantly. If two microphones pick up the same drum hit at slightly different times, the waves can cancel each other out, making the drum sound thin and weak. This is a "Phase Issue".

4. Trig Identities (The Toolbox)

Identities are equations that are true for ANY angle. They are the "hacks" of calculus.

The Pythagorean Identity:
sin²θ + cos²θ = 1
This looks fancy, but it is literally just a² + b² = c² applied to the Unit Circle (where c=1). If you know sin, you can always find cos.

Double Angle Formulas:
sin(2θ) = 2sin(θ)cos(θ)
These are critical in Calculus when you need to make an equation simpler to integrate.

5. Inverse Trig: Finding the Angle

Regular trig functions take an Angle and give you a Ratio (Side length).
Inverse trig functions (Arcsin, Arccos) take a Ratio and give you the Angle.

Engineering Problem: You have a ladder 10m long leaning against a wall. The base is 6m from the wall. What is the angle?
• You have Adjacent (6) and Hypotenuse (10). Use Cosine.
• cos(x) = 6/10 = 0.6.
• x = arccos(0.6) ≈ 53.1 degrees.

6. Game Development & Aiming

Video games run on Trig.
The "Look At" Problem:
You are a sniper at (x1, y1). The enemy is at (x2, y2). What angle should your gun rotate to face them?

You calculated the difference in x (dx) and y (dy).
Angle = arctan(dy / dx)

But wait! Normal calculators fail if dx is negative (behind you). Game developers use a special function atan2(y, x) which handles all 360 degrees perfectly. Without this, enemies would shoot backwards half the time.

7. GPS and Triangulation

Your phone knows where you are because of satellites. A single satellite knows you are "somewhere" 20,000km away (on a sphere). Two satellites narrow it down to a circle intersection. Three satellites narrow it down to two points. Four satellites pinpoint you exactly.

This is Triangulation (using triangles to find location). The speed of the radio signal is the "Hypotenuse".

8. FAQ

Q: Degrees vs. Radians?
A: Degrees are for humans (360 is a nice number). Radians are for math/nature (2π is the actual ratio of circle to radius). Always use Radians in Calculus.

Q: Why is Tan(90) undefined?
A: Tan = Sin/Cos. At 90 degrees, Cos is 0. You cannot divide by zero. The slope of a vertical line is infinite.

Conclusion

Trigonometry allows us to convert circular motion into linear coordinates. It bridges the gap between algebra and geometry. Next time you see a triangle, don't just see shapes—see the ratios that hold the universe together.